Batch 2 - Class 284 - Pilgrim's Puzzle

Zoom: send meeting Id and password

Start recording

Preclass Exercise:

(Dudeney - 230) Here is a pretty little puzzle that only requires twelve pennies or counters. Arrange them in a circle, as shown in the illustration. Now take up one penny at a time and, passing it over two pennies, place it on the third penny. Then take up another single penny and do the same thing, and so on, until, in six such moves, you have the coins in six pairs in the positions 1, 2, 3, 4, 5, 6. You can move in either direction round the circle at every play, and it does not matter whether the two jumped over are separate or a pair.

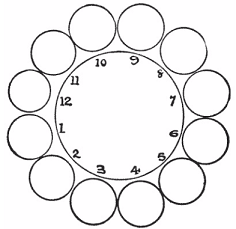
Answer: 12->3, 7->4, 10->6, 8->1, 9->5, 11->2
What if we wanted them to jump two stacks of pennies, regardless of number of pennies in that stack?

Answer: 10->1, 9->6, 11->2, 8->5, 12->3, 7->4

Attendance: Raghav, Kabir, Shikhar, Ayush, Rhea Chadha, Ryan Chadha, Rohan, Yatharth, Anika, Vansh, Adyant, Dhriti, Ekagra, Mihir, Advay, Aneesh, Siddharth, Tarush, Aarav, Vivaan, Anshi, Aarush

Class Notes:

A pilgrim arrives in Duona, a sixteen-block town created by five streets running north-south that intersect with five streets running east-west. Like all pilgrims, she arrives in the northwest corner of town, and needs to make her way to a shrine in the southeast corner. Unfortunately for the pilgrim, Duona imposes a tax system on visitors, charging 2 silver pieces for each block walked to the east, and doubling what you owe every time you walk south. To make the payment system fairer and encourage longer stays, they subtract 2 silver pieces for each block walked to the west, and halve what you owe when you walk a block north. The townsfolk keep track of your path, and you must pay in full on your arrival in the southeast corner.

What is the most expensive path that you found?

E, E, E, E, S, S, S, W, W, W, N, E, S, S, W, W, N, N, N, E, E, E, S, S, S, E (170 coins) non repeating

What was the cheapest path that you found?
What advice would you give pilgrims about how to pay the least amount for their journey?
There’s a rumor that there’s a way to travel through the town and owe zero at the end. Test if this rumor is true and confirm or deny this rumor. Explain your thinking.
There’s another rumor that there’s a way to travel through the town and make money by the end of the journey. Test if this rumor is true and confirm or deny this rumor. Explain your thinking.

SSSS-E-N-EEE-NNN-WWW-SS-EE-N-W-SSS-EEE gets profit of 78

Can the pilgrim accomplish the above without traveling the same segment of street more than once?

Zero outcome - SSEEENWWSSESEE with no repetitions
E, S, E, E, S, W, W, S, E, E, E, N, N, N, W, W, S, S, S, S, E, E seems to be longest length non-repeating path (22)

Put "+" signs between digits 9 8 7 6 5 4 3 2 1 to get 99. You are not allowed to change the sequence of digits. You may choose to not put any sign between some digits, for example you could use 98+7... kind of formation

Answer: 9+8+7+65+4+3+2+1 9+8+7+6+5+43+21

Homework Problem:

There are balls of 10 different colors. All balls are of 10gm each, except one color which are all either 9gm or 11gm (we do not know for sure). There is a weighing scale where we can put any number of balls and read the weight. In one weighing, figure out which balls are odd weight, and whether they are lighter of heavier than others.

Answer: Take 1 ball of 1st color, 2 balls of 2nd color, and so on. Weigh the 55 balls. The difference of weight from 550gm is the pile from which those balls were taken. The weight being more or less than 550 denotes heavier or lighter balls resp.

Instructor Notes: Kids typically will start at choosing 1 ball of each color. Then try to get to to different number of balls.

What if we knew that exactly two stacks were defective (in the same way)?

Answer: We can map the possibilities - we land up with the Fibonacci sequence

What if any number of stacks could be defective?

Answer: We can map the possibilities - we land up with powers of 2. Note that this is a generalized solution, so subsumes the previous two problems as well

References:

Daniel Finkel's Pilgrim's Puzzle (https://wordplay.blogs.nytimes.com/2013/08/26/pilgrim/)

Mathematics.pdf - Dudeney

Mathematical Circles (Russian Experience), by Dmitri Fomin, Sergey Genkin, Ilia Itenberg